앞선 퀴즈의 배경이 되는 개념을 이야기하고자 한다.
다소 이론적이며 재미없을 수도 있지만, 가끔은 진지한 수학 얘기도 필요하다고 생각한다.
예전에는 “평면분할이론”이라고 했었는데, 다시 검색해 보니, 잘 안 보인다. 아마도 이름이 바뀌었나 보다.
시작은 단순하다.
한 평면이 있고, 그 위에 직선들을 그을 때, 평면을 최대한 많은 수로 분할하는 방법은 무엇인지에 관한 질문이다.
우선, 지금 보이는 화면을 하나의 평면이라고 한다면, 직선을 하나 그어보면 다음과 같다.
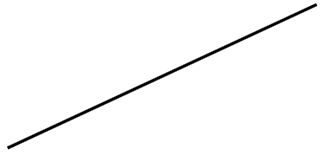
직선은 양 끝으로 무한이 뻗어 나가므로, 이 직선에 의해 평면은 둘로 나뉘게 된다. 이번엔 직선 두 개로 하면 어떻게 될까?
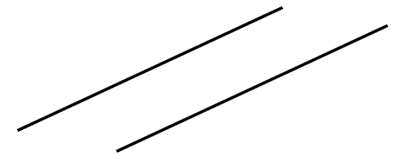
이렇게 긋는다면 평면은 3개로 분할된다. 하지만, 질문은 최대한 많은 수로 분할하라고 했으니, 이는 정답이 아니다.
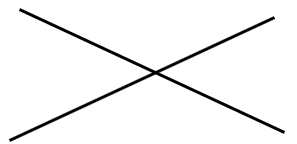
이렇게 하면 두 개의 직선으로 평면을 4개로 분할할 수 있다. 3개보다 4개가 많으니, 이것이 정답이 된다. 조금 더 가보자.
이번엔 3개의 직선으로 분할하면 어떻게 될까?

직선 3개를 위와 같이 그으면 보다시피 평면은 4개 혹은 6개로 분할이 된다. 따라서 6개가 정답이라고 생각할 수 있지만, 아니다, 더 나온다.
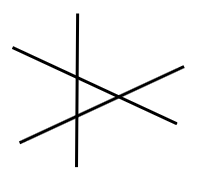
그림과 같이 배치한다면 평면은 7개로 분할이 되므로, 이것이 정답이 된다.
그럼 이제 정리해 보자. 어떻게 하면 가장 많은 분할을 만들어 낼 수 있을까?
일일이 다 시도해 볼 수는 없는 노릇이다. 여기에 이론이 있다.
이 개념이 소개된 책에는 다소 어려운 말로 표현이 되어 있는데, 그냥 쉽게 말하자면 새로 긋는 직선은 기존에 그어진 직선과 평행하지 않고, 기존의 교점을 지나지 않으면 된다. 위 직선 3개 그림에서 첫 번째처럼 평행하지 않게, 두 번째 그림처럼 교점 지나지 않게 그린 것이 세 번째 그림인 것이다. 그렇다면, 직선 5개로는 과연 어떻게 하면 될까? 이것이 바로, 앞선 글에 소개된 퀴즈와 연결이 되는 내용이다.
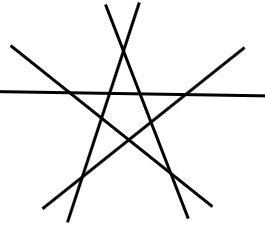
하나하나씩 직선을 그려보면, 먼저 그린 직선과 그 어느 것도 평행하지 않고, 그 어느 것도 이전의 교점을 지나지 않는다.
한 발짝 더, 이렇게 하다 보니, 직선이 늘어날수록 새로 만들어지는 교점의 개수와 분할되는 면의 수들 간의 관계에서 일정한 규칙이 보이게 된다. 아래 표를 보자.
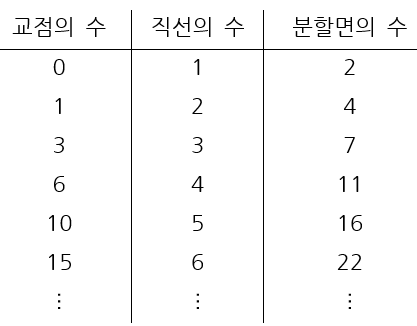
아마도 눈치가 빠른 사람은 알아볼 수 있다.
아직 잘 안 보이는 사람들을 위해 표에 화살표를 추가해 본다.
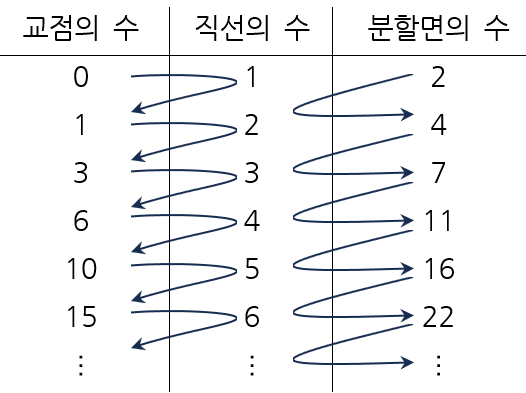
자, 이제 모두들 알아볼 수 있을 것이다. 화살표 흐름대로 더하면 다음 숫자가 나타난다. 이 또한 수열로 연결 지어 설명할 수 있지만, 이쯤 하고.
최대한 간단하게 설명을 하느라고 했으니, 대부분 이해할 수 있으리라 본다. 수업시간에 아이들도 대부분 이해한다. 더 깊이 파고들면 어려운 내용이 많지만. 거기까진 안 가도 사는데 지장 없다. 이 정도만 안다고 해도 도형문제 접근에 이따금씩 도움이 되는 순간들이 있을 수 있다. 예전 tvN 프로그램 중에 “문제적 남자” 가 있었는데, 언젠가 도형문제가 이걸로 풀린 적이 몇 번 있었다.
이로써 지난 퀴즈에 대한 이론적 배경 설명을 마치겠다.
#수학 #도형 #평면분할이론 #직선 #최대로평면분할 #문제적남자 #퀴즈해설
'수학공부' 카테고리의 다른 글
| 부모님들은 공부를 왜 하라고 할까? (2) | 2024.02.27 |
|---|---|
| 성적의 상대성 이론(?) (1) | 2024.02.22 |
| 수학 퀴즈~~!! (1) (2) | 2024.02.06 |
| 과제는 받은 당일에 완료하도록 하자~!! (7) | 2024.02.01 |
| 수업과 공부를 구별하라~!! (0) | 2024.01.30 |
